Submitted by Ruthmae Sears, University of South Florida; Orly Buchbinder, University of New Hampshire
Technological tools can be used in teacher preparation programs to develop students’ conceptual understanding of the properties of polygons and to communicate appropriate vocabulary (Kartal & Çınar, 2024). The exploration opportunities afforded using technological tools, such as Desmos, can help students develop conceptions of shapes, engage in informal deduction, and enhance their mathematical vocabulary (Herman, 2022). This article describes how graduate students in a mathematics education teacher preparation program engaged in a card sort exercise to describe properties of polygons using a Desmos activity (https://teacher.desmos.com/activitybuilder/custom/67224d9437c8fd0a42d4c764).
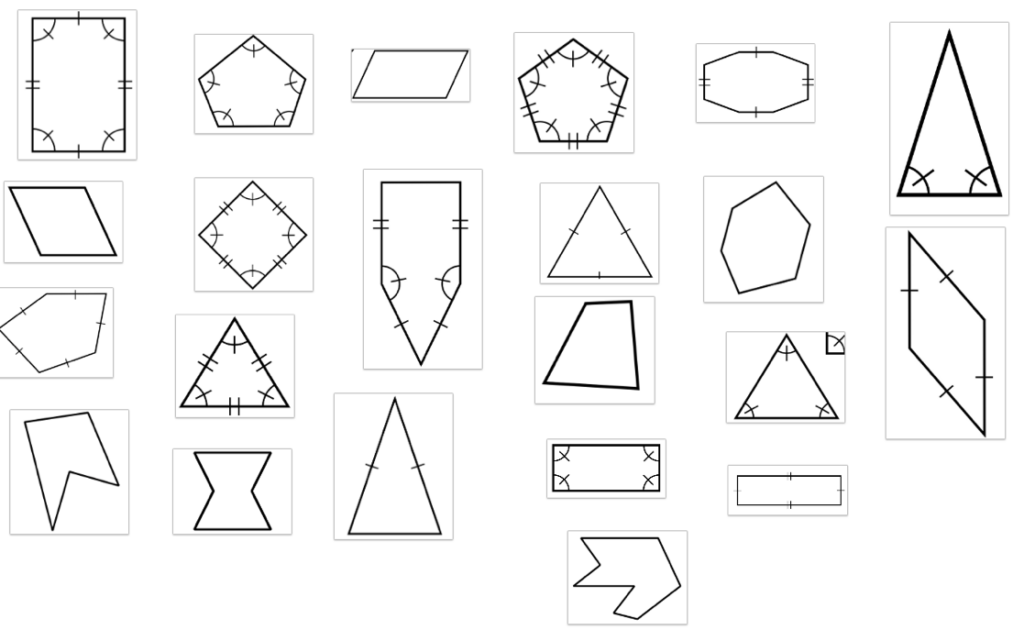
The data were collected in Spring 2024 from four students at a university located in the southeastern region of the United States. The students were assigned to complete a polygon card sort activity, which was designed to develop their geometric vocabulary and incorporate the following terms: convex, concave, regular, equiangular, and equilateral (Brown, n.d.). Particularly, the students were asked to sort the polygons in Figure 1 using their preferred grouping criteria and to explain the rationale for their grouping. They were then asked to sort the same cards using different grouping criteria and to provide reasoning. Afterward, the students were presented with sorted polygons as “convex,” “concave,” “equilateral,” “not equilateral,” “equiangular,” “not equiangular,” “regular,” and “not regular polygons,” and students were asked to provide an explanation of what the terms “convex,” “concave,” and “regular” meant (Brown, n.d).
Figure 1. Polygons in card sort activity (Brown, n.d.).
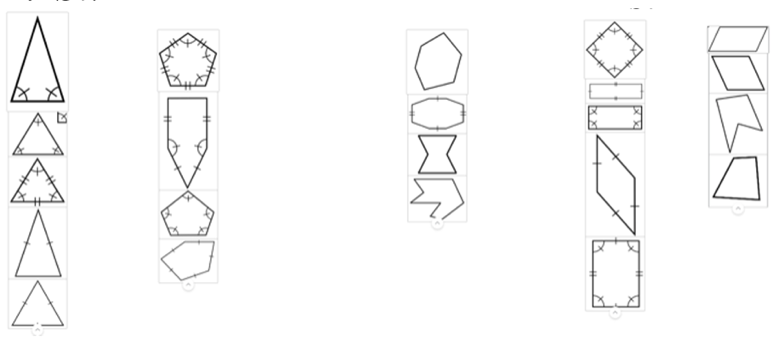
This activity was rich in having students consider the properties of polygons as it helped strengthen their vocabulary of geometrical concepts. However, the students struggled to use proper terminology to justify their thoughts and explain their thinking robustly. For instance, during the first sorting attempt, the students grouped the polygons based on the number of sides or by the mere presence of the markings on the polygons. Interestingly, the students did not attend to the symbolic meaning of these markings as representing equiangular or equilateral properties. Instead, students referred to the presence and positioning of the markings on sides or angles. This suggests a superficial sorting that does not attend to the properties of polygons but only to the perceptual features of the diagrams. For instance, for Figure 2, Student A indicated:
“The first group I made was all the triangles. Then, I combined all the pentagons. Next, I grouped together any polygon with greater than 5 sides. Lastly, I split the quadrilaterals between two groups. One group is any quadrilateral with congruent sides or angles. The other group is any quadrilateral without congruent markings.”
Figure 2. Student A’s first grouping
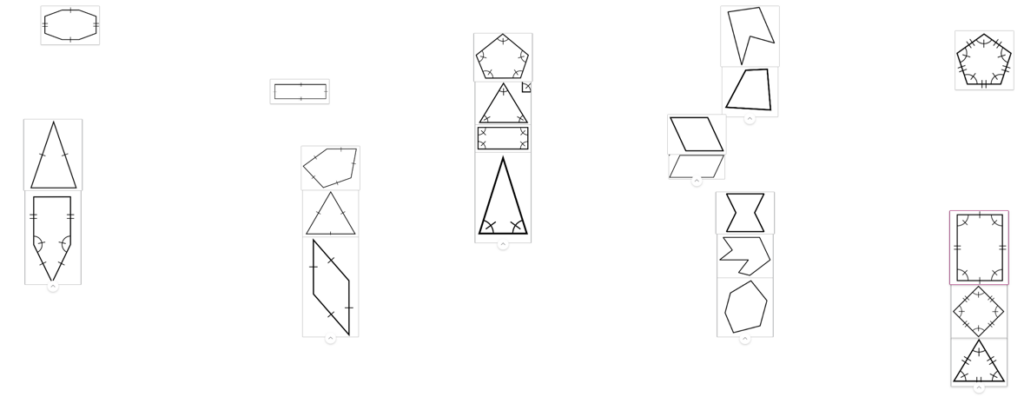
In a similar fashion, Student B explained that they sorted the polygons based on the visual clues:
“I sorted by grouping:
– All shapes that have all information given (sides, angles)
– shapes that have only information about the angles
– shapes with no given information
– shapes with only information on the sides
– shapes with some information given”
Figure 3. Student B’s work on the first grouping.
These examples show that the vocabulary utilized by students for justifying their first polygon sorting was limited. It avoided descriptive phrases and mathematical terminologies that attend to the geometric features and properties of polygons, as the task intended. This suggests that in this first sorting, the students were operating at level 1 (visualization) of the van Hiele Model of Geometrical Thought (Armah et al, 2018) because they focused primarily on visualization, with minimal progress in the analysis level of classifying shapes by their properties.
For the second grouping, there was a slight improvement in the usage of geometrical terms. As an example, Student C indicated that,
“First, I made the grouping of convex polygons with no given angles or congruent sides. Second, I classified concave polygons. Next, I grouped any polygon with only congruent sides. Then, I added a class for both all congruent sides and angles (partial definition of triangle, square, and pentagon). Lastly, I grouped full definitions of a triangle, square, rectangle, and pentagon).”
Figure 4. Student C’s work on the second grouping.
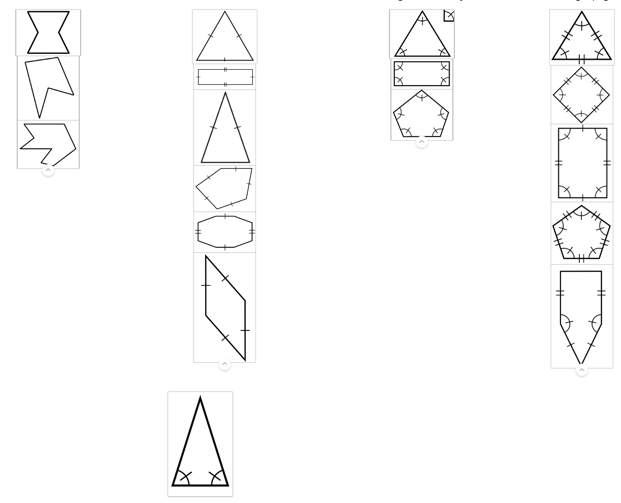
In this response, we observe the use of geometry vocabulary (concave, convex, congruent) as well as some polygon names. The vague term “partial definition” was interpreted as an improper attempt to refer to features of regular polygons, which are both equiangular and equilateral. Student’s C grouping of information by either sides or angles was conveyed as “partial definition,” whereas, the presence of marking of both angles and sides was referred to as “full definition.” This (mis)use of the terms suggests a fragile conception of polygons and their properties.
When students were given the sorted polygons grouped by specific geometric categories, they were asked to explain the meaning of certain terms, like concave and convex. Student A wrote: “Concave polygons represent those that ‘cave’ inwards to the interior of the shape. The convex polygons do not have this aspect.” While this way of thinking can be helpful as a mnemonic device to recall or help students recall the term “concave,” it would be valuable if the student would be able to provide a more precise mathematical definition of “concave,” although not necessarily a formal definition. Student C came closer to using the definition of “concave,” while still making an imprecise claim, saying: “The convex polygons have no line containing a side that has a point within the interior of the figure while concave (non-convex) polygons do have at least one line that passes within the interior.” A more precise definition for a convex polygon is that every segment connecting two points within the polygon lies entirely within the polygon. There seems to be an attempt to use proper mathematical vocabulary. However, the terms are not appropriately defined.
Some definitions seem easier for students to explain. For example, to define equiangular and equilateral with a great degree of precision, Student A noted: “Equilateral means that all of the sides in the polygon are congruent to each other. Equiangular means that all of the angles in the polygon are congruent to each other.” This comes closer to van Hiele level 2 (analysis). Given that the van Hiele model of geometrical thinking suggests that individuals learn geometry across five levels (visualization (level 1), analysis (level 2), abstraction (level 3), deduction (level 4), and rigor (level 5)) it appears that the depth of knowledge exhibited were generally rudimentary.
Following this activity, an instructor (the first author of this paper) engaged students in a rich mathematical discussion, helping them clarify the meaning of geometric terms and use proper vocabulary. Additionally, the students engaged in didactical discourse around the implications of attending to precision by both teachers and students in geometry classrooms. The students were encouraged to reflect on their responses from a teacher’s perspective and provide pedagogical recommendations to enhance the description of the groupings and deepen their geometrical understanding. This strategy aligns with Student Learning Objective 3 (SLO-3) (Get: A Pencil, 2022), which suggests that “Future secondary geometry teachers must deeply understand specialized content that is aligned to national and state secondary standards, know the best practices for teaching the content, and be able to reflect on their teaching.”
The ways in which future teachers and graduate students define terms have implications for their abilities to communicate and conceptualize a geometric concept, reason, and produce proofs. Thus, attention is needed to develop their geometric vocabulary. The results suggest that the students struggled to provide detailed descriptions to justify their grouping of polygons. GeT course instructors should attend to students’ development of geometrical understanding progression and provide opportunities for students to advance across van Hiele levels of Geometric Thought.
References
Armah, R. B., Cofie, P. O., & Okpoti, C. A. (2018). Investigating the effect of van Hiele phase-based instruction on pre-service teachers’ geometric thinking. International journal of Research in Education and Science, 4(1), 314-330.
Brown, R. Polygons Card Sort. https://teacher.desmos.com/activitybuilder/custom/67224d9437c8fd0a42d4c764
Get: A Pencil: Student Learning Objective 3 (SLO 3). – Secondary geometry understanding. https://getapencil.org/learning-objective-3/#summary
Kartal, B., & Çınar, C. (2024). Preservice mathematics teachers’ TPACK development when they are teaching polygons with GeoGebra. International Journal of Mathematical Education in Science and Technology, 55(5), 1171-1203.
Herman, T., Suryadi, D., & Prabawanto, S. (2022). Concept of polygon: Case study of elementary students’ difficulties. Mathematics Teaching Research Journal, 14(5), 34-47.
